14565번: 역원(Inverse) 구하기
집합 Zn을 0부터 n-1까지의 정수 집합이라고 하자. Zn ∋ a, b, c 일 때, (a+b) mod n = 0이면 b는 a의 덧셈역이라고 하고 (a*c) mod n = 1이면 c는 a의 곱셈역이라고 한다. 정수 N, A가 주어졌을 때 Zn에서의 A의
www.acmicpc.net
나머지 연산의 덧셈 역과 곱셈 역을 구하는 문제입니다. 덧셈역은 쉽게 구할 수 있지만 곱셈 역은 구하기 어려워보입니다.
1. 덧셈역 구하기
어떤 수 A와 M을 안다고 가정할 때, A%M을 0으로 만드는 덧셈 역 C는 M-A입니다.
이는 생각해보면 매우 간단합니다. 아래의 예를 볼까요?
5 % 13 = 5입니다.
13 % 13 = 0입니다.
(5 + C) % 13 을 0을 만드는 C는 당연하게도 13-5가 됩니다.
수의 범위에 주의하며, M-A를 출력하는 코드를 작성하면 덧셈역 구하기는 해결할 수 있습니다.
2. 곱셈역 구하기
확장 유클리드 알고리즘을 사용하면 곱셈 역을 구할 수 있습니다.
이 알고리즘을 설명하기에 앞서, 곱셈역이 무엇인지 알아보도록 하겠습니다.
(A*C) % M = 1을 만족시키는 C를 A에 대한 곱셈역이라고 합니다(A와 M을 안다고 가정).
그럼 확장 유클리드에 대한 식을 보겠습니다. 동공이 흔들리고 침대에 드러눕고 싶어진다면 정상입니다.
하지만 괜찮아요. 저는 아직도 이 식을 보면 울렁거립니다.
다음과 같은 식으로 곱셈 역을 구할 수 있습니다.
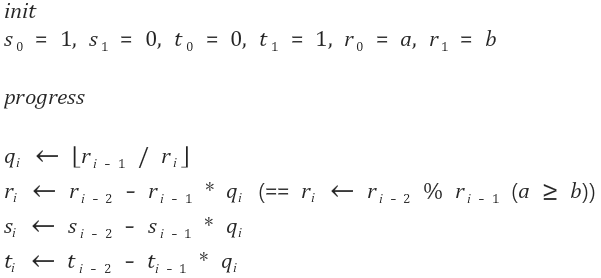
알고리즘 교수님이 이런 말씀을 하셨습니다. 결국 세상은 문과가 지배한다고. 문제를 잘 읽고, 관련 자료가 영어로 나와도 긴장말고 잘 읽으라는 뜻으로 하신 말씀입니다. 저는 교수님이 달을 가리킬때 손가락만 바라본 것 같습니다.
그럼 찬찬히 뜯어봅시다.
(2.2)에서는 변수들의 초기화 조건을 명시하였습니다. 벡터를 사용하여 다음과 같이 초기화 할 수 있을 것 같습니다.
ll extended_euclid(ll n, ll a)
{
vector<ll> Si = { 1,0 };
vector<ll> Ti = { 0, 1 };
vector<ll> Ri = { n, a };
ll Qi = n / a ;
ll r1, r2, temp;미완성 코드이므로 대괄호를 닫지 않았습니다. ll은 long long으로 정의하였습니다.
이 알고리즘의 종료 조건은 Ri가 0이 되었을 때 입니다. Ri가 0이 되면 마지막 Ti를 반환합니다. 이는 A를 N으로 나는 나머지의 곱셈 역이 됩니다. 그럼 완성 코드를 살펴봅시다.
ll extended_euclid(ll n, ll a)
{
vector<ll> Si = { 1,0 };
vector<ll> Ti = { 0, 1 };
vector<ll> Ri = { n, a };
ll Qi = n / a ;
ll r1, r2, temp;
while (1)
{
r2 = Ri[Ri.size() - 2];
r1 = Ri[Ri.size() - 1];
temp = r2 % r1;
Ri.push_back(temp);
if (temp==0) return Ti[Ti.size()-1];
Qi = r2 / r1;
Si.push_back(Si[Si.size() - 2] - Si[Si.size() - 1] * Qi);
Ti.push_back(Ti[Ti.size() - 2] - Ti[Ti.size() - 1] * Qi);
}
}근데 이 알고리즘이 정말로 작동할까요?
저는 소싯적 학원 조교들에게 괜히 어려운 수학 문제를 물어본 적이 있습니다. 나는 답을 아는데, 당신도 답을 구해낼 수 있을까? 라는 미성숙한 질문을 던져 속으로 조교님들을 테스트한 것이죠. 이 알고리즘에도 적용시켜봅시다. 다만, 답을 알고 있는 상태로, 이 알고리즘이 답을 도출하는지 확인해보겠습니다.
A = 6, N = 13일 때, A의 역원은 11입니다.
[초기화 단계]
| i | Si | Ti | Ri | Qi |
| 0 | 1 | 0 | 13 (n) | 2 (n/a) |
| 1 | 0 | 1 | 6 (a) |
[종료 조건 확인]
| i | Si | Ti | Ri | Qi |
| 0 | 1 | 0 | 13 | 2 |
| 1 | 0 | 1 | 6 | |
| 2 | 1(13%6) |
아직 종료 조건인 Ri==0을 만족하지 못했습니다. 다음 연산을 수행합니다.
[연산 수행]
| i | Si | Ti | Ri | Qi |
| 0 | 1 | 0 | 13 | 2 |
| 1 | 0 | 1 | 6 | |
| 2 | 1 (1 - 0*6) | -6 (0 - 1*6) | 1 |
[종료 조건 확인]
| i | Si | Ti | Ri | Qi |
| 0 | 1 | 0 | 13 | 2 |
| 1 | 0 | 1 | 6 | |
| 2 | 1 | -2 | 1 | |
| 3 | 0 (6%1) |
Ri의 마지막 값이 0이 되었습니다. 종료 조건을 만족하여 Ti를 반환합니다.
엥? 이상하지 않나요? Ti의 값은 11이 나왔어야하는데, 정작 이 코드에서는 -2를 반환합니다. 하지만 괜찮습니다.
결과가 음수라면, 양수가 나올 때 까지 N값을 더해줍니다.
우리는 모듈러 연산을 수행중이므로, 결과값에 N값을 아무리 많이 더해도 결국 같은 값을 얻을 수 있습니다. 다음 예를 보시면 무릎을 탁 칠수 있으실 것 같습니다.
3 % 13 = 3
(3+13) % 13 = 16 % 13 = 3
(16 + 13) % 13 = 29 % 13 = 3
따라서, (-2+13) % 13 = 11 % 13 = 11
이해가 좀 되실까요? 그럼 정답 코드를 보겠습니다.
3. 정답 코드와 설명
#include <iostream>
#include <algorithm>
#include <vector>
#define ll long long
using namespace std;
ll gcd(ll n, ll a)
{
if (a == 0) return n;
return gcd(a, n % a);
}
ll extended_euclid(ll n, ll a)
{
vector<ll> Si = { 1, 0 };
vector<ll> Ti = { 0, 1 };
vector<ll> Ri = { n, a };
ll Qi = n / a ;
ll r1, r2, temp;
while (1)
{
r2 = Ri[Ri.size() - 2];
r1 = Ri[Ri.size() - 1];
temp = r2 % r1;
Ri.push_back(temp);
if (temp==0) return Ti[Ti.size()-1];
Qi = r2 / r1;
Si.push_back(Si[Si.size() - 2] - Si[Si.size() - 1] * Qi);
Ti.push_back(Ti[Ti.size() - 2] - Ti[Ti.size() - 1] * Qi);
}
}
int main()
{
ll n, a;
cin >> n >> a;
cout << n - a << " ";
if (gcd(n, a) != 1)
{
cout << -1;
return 0;
}
ll ret = extended_euclid(n, a);
while (ret < 0)
{
ret += n;
}
cout << ret;
return 0;
}우선 GCD를 수행하여, A와 N이 서로소인지 확인하고 확장 유클리드 알고리즘을 적용합니다.
유클리드 알고리즘의 반환값 ret이 음수인지 확인하고, 양수가 될 때 까지 N값을 더해주는 모습을 보실 수 있습니다.
항상 무언가를 공부하며 드는 생각이 있는 것 같습니다.
이걸 배워서 어디에다 써먹을 수 있을까?
어디에 적용될지는 몰라도, 다음 문제는 도전해볼 수 있을 것 같습니다.
이 문제도 한번 풀어보세요.
20412번: 추첨상 사수 대작전! (Hard)
한 줄에 걸쳐 준표가 좋아하는 소수 m, 참가자들이 정한 Seed, 시연으로 공개된 X1, X2 이 주어진다. 항상 가능한 상황만 입력으로 주어진다.
www.acmicpc.net
만약 이 문제에서 막힌다면 제 포스트가 도움이 될 수 있을 것 같습니다.
'알고리즘' 카테고리의 다른 글
| [BOJ] 15649번. N과 M(1) (0) | 2021.01.10 |
|---|---|
| [BOJ] 1012번. 유기농 배추 (0) | 2021.01.10 |
| [BOJ] 1654번. 랜선 자르기 & 수 찾기 (0) | 2021.01.10 |
| [BOJ] 1193번. 분수찾기 (0) | 2021.01.10 |
| [2020 APC] 추첨상 사수 대작전!(Hard) 풀이 (0) | 2021.01.03 |
