0. 잡설
이번에 배포를 위한 서버를 제작하던 중, 보안에 대한 이슈가 많았습니다.
기존 개인 프로젝트를 하면서 신경쓰지 않았던 부분이라 좋은 경험을 하게 되었습니다.
HTTPS, 즉 SSL보안을 적용시켜야 한다고 생각했고, 이에 관해 동작 원리를 알고 싶어 정리합니다.
'정보보호'과목에서 배웠던 이론을 기초로 나름 제 언어로 정리해보겠습니다.
1. SSL(HTTPS)보안이 필요한 이유
2학년 시절, 간단한 웹소켓 채팅 웹을 만들어 Wire shark로 패킷을 검사해보는 프로젝트가 있었습니다.
SSL보안을 적용하지 않고 HTTP로 프로젝트를 진행했었습니다.
HTTPS로는 패킷 검사하는 것이 힘드니까요.
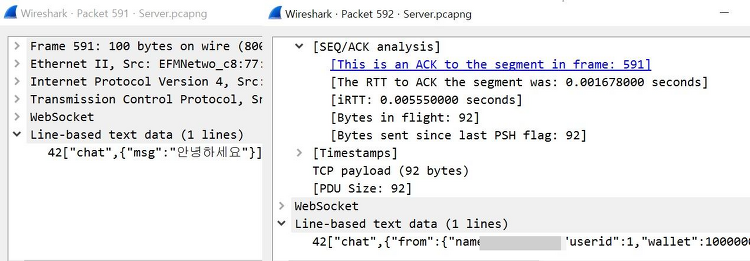
HTTP로 접속했을 때 패킷을 중간에 누군가가 까본다면 어떻게 보일까요?
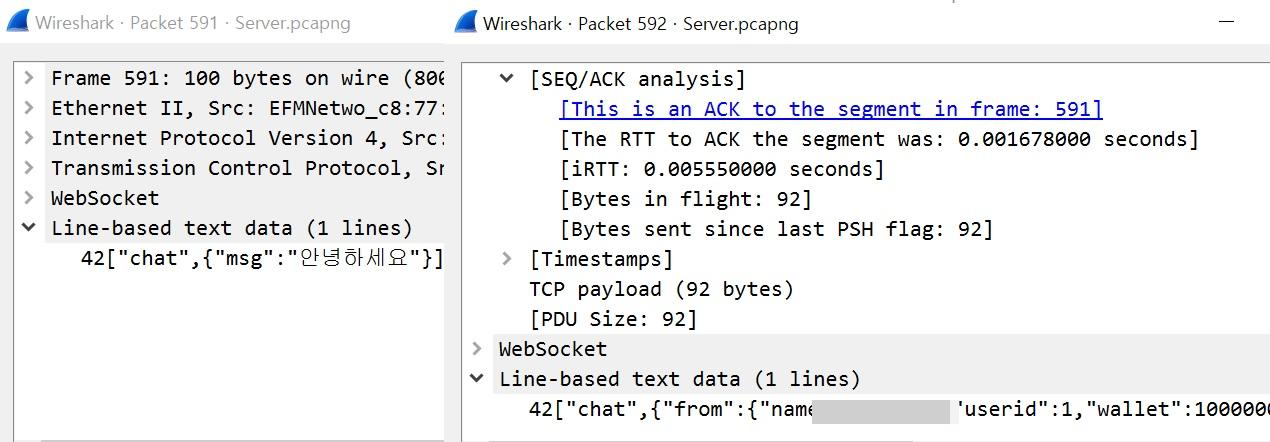
이렇게 왼쪽 msg처럼, "안녕하세요"라는 패킷이 그대로 복원이 됨을 알 수 있습니다.
패킷에 비밀번호가 그대로 전달되거나, token이라도 전달된다면 중간자가 사용자 행세를 할 수도 있겠습니다(이를 Packet sniffing 공격이라고 합니다).
따라서 우리는 클라이언트와 서버가 비밀통로로 연결되는 SSL보안 연결이 필요합니다.
2. 대칭키와 비대칭키
SSL연결은 기본적으로 비대칭키로 암호화를 진행하지만, 우선 연결이 되면 대칭키로 빠르게 내용을 주고 받으므로 두개의 개념을 모두 알고 있어야 합니다.
대칭키
어떤 문장을 암호화 하는 사람과 해독하는 사람(복호화)하는 사람이 모두 같은 키를 사용하는 방식입니다.
예를 들어, 시저 암호화가 있습니다. 알파벳이 있다면, 3글자씩 밀려 써서 암호화를 하는 방식입니다.
표로 살펴보겠습니다.
| 원문 | A | B | C | D | E | ... | X | Y | Z |
| 암호화시 | D | E | F | G | H | ... | A | B | C |
만약 시저 암호화를 한 메시지가 다음과 같았다고 합시다.
L FDPH L VDZ L FRQTXHUNG
암호화는 각 알파벳을 3칸 밀어서 쓴다는 것을 아는 해독자는 이를 다음과 같이 복호화 할 수 있습니다.
I CAME I SAW CONQUERED
대칭키 암호화의 원리는 이렇습니다. 암호화하는 방식과 복호화 하는 방식(키)이 동일한 것입니다.
물론, 현대에는 비트를 알고리즘에 의해 옮기는 방법으로 더 복잡합니다. 하지만 이 역시도 알고리즘이 공개되어있기 때문에 brute force공격을 하면 언젠가는 뚫리게 되어 있습니다.
현대 암호를 풀려면 얼마나 시간이 걸릴까요?
현대적인 대칭키 암호화 방식인 DES를 3중으로 쌓으면 2^112의 brute force공격이 필요합니다.
이는 이정도의 크기를 가집니다.
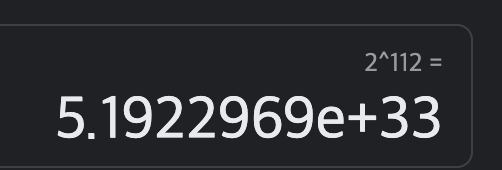
아주아주 좋은 컴퓨터가 저 만큼만 brute force공격을 한다면 대칭키는 뚫리게 되는 것이죠!
은행 보안 카드가 몇 초에 한번씩 업데이트되는 이유가 여기에 있습니다. 아주아주 좋은 컴퓨터가 브루트포스로 공격을 진행해도, 결과가 나오기 전에 키를 바꾸어 버리는 것이지요!
. . .
이 방식은 정해진 몇개의 암/복호화 알고리즘을 수학적으로 따르면 되므로, 속도가 빠릅니다.
하지만, 암호를 전달하는 과정에서 키가 탈취되는 문제가 있습니다. 암호 키를 전달하는 과정 자체에서 암호키가 가로채질 수 있다는 것입니다.
장점: 암/복호화가 빠르다
단점: 키 전달 과정에서 탈취될 수 있다.
비대칭키
공개키 알고리즘이라고도 합니다. 공개키 알고리즘이 더욱 와닿으니 앞으로 공개키라고 설명하겠습니다.
어떤 메시지를 암호화해야한다고 합시다. 비대칭키 알고리즘에서는 개인키/공개키로 암호화됩니다.
어떤 메시지가 Alice에 의해 암호화된다고 할 때, 메시지는 Alice의 공개키로 암호화되고, 복호화 시에는 Alice의 개인키로만 복호화될 수 있습니다.
누구나 Alice의 공개키를 가질 수 있어 Bob도, 스폰지밥도, 징징이도 암호화를 할 수 있지만 메시지의 복호화는 Alice만이 가지고 있는 개인키로만 가능합니다. Alice만 읽을 수 있게 되는 것이죠!
공개키는 단방향 함수로 암호화됩니다. 단방향 함수라 함은, 한 방향으로 계산은 쉬우나 반대 방향으로의 계산은 어려운 함수를 의미합니다.
예를 들어, 3*17 = 51이라는 것은 아주 쉬우나, 51 = 3*17이라는 사실은 알아내기 매우 어렵습니다.
N=pq라는 계산은 용이하지만 N이 주어졌을 때 P와 Q를 알아내는 것은 쉽지 않은 것이 단반향 함수입니다.
비대칭키에 대한 가장 유명한 방식은 RSA방식입니다. 바로 RSA방식에 대해 공부하면 머리가 아플 수 있으므로, 이해하기 쉬운 냅색 문제로 비대칭키 암호화를 하는 경우를 보겠습니다.
냅색 문제와 비대칭키 알고리즘
냅색 문제란?
가중치 집합 {62, 93, 26, 52, 166, 48, 91, 141}이 주어졌다고 합시다.
가중치 집합의 원소를 합쳐서 302이 되는 subset을 찾아봅시다.
일반적으로 냅색 문제는 NP-complete입니다. 어떤 문제가 NP-complete라는 말은, 그 문제를 시간만 많이 주면 풀어낼 순 있지만 문제의 답을 찾는 알고리즘은 밝혀지지 않았다는 뜻입니다. 더 쉽게 말하면 인간은 풀 수 있지만 컴퓨터로는 못푸는 문제라고 생각할 수 있습니다.
위의 문제의 답은 62+26+166+48 = 302 입니다.
냅색 문제를 쉽게 풀어내는 방법은 superincreasing knapsack문제로 바꾸어 푸는 것입니다. 이는 "새로운 가중치는 모든 이전 가중치의 합 보다 크다"라는 의미입니다.
예를 들어 가중치 집합이 {2, 3, 7, 14, 30, 57, 120, 251}인 경우
이 방법으로 합이 186인 subset을 찾는 문제의 답은 2+7+57+120 = 186입니다.
이제 본격적으로 냅색 알고리즘을 활용하여 암호화를 해보겠습니다.
공개키는 가중치 집합이고,
개인키는 공개키를 Superincreasing knapsack문제로 풀어낸 집합과 conversion factor입니다.
예를 들어, 본인이 Superincreasing kanpsack문제의 해 집합을 가지고 있다고 해봅시다.
superincreasing Key = {2, 3, 7, 14, 30, 57, 120, 251}
또한 m=41, n=491, 1/m % n = 41^-1 mod 491 = 12이라는 변환 팩터를 가지고 있습니다.
이 키와 변환 팩터를 가지고 다음과 같이 공개키를 제작할 수 있습니다.
2 X 41 mod 491 = 82
3 X 41 mod 491 = 123
7 X 41 mod 491 = 287
14 X 41 mod 491 = 83
...
120 X 41 mod 491 = 10
251 X 41 mod 491 = 471
그러면 공개키는 다음과 같습니다.
공개키: {82, 123, 287, 83, 248, 373, 10, 471}
그럼 이를 어떻게 써먹을 수 있을까요??
예를 들어 10010110을 암호화 한다고 합시다.
| 공개키 | 82 | 123 | 287 | 83 | 248 | 373 | 10 | 471 |
| 평문 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
암호화 결과는 82 + 83 + 373 + 10 = 548입니다.
그럼 548로 암호화된 키를 복호화 하려면 다음과 같이 하면 됩니다.
개인키 = {2, 3, 7, 14, 30, 57, 120, 251}
또한 m=41, n=491, 1/m % n = 41^-1 mod 491 = 12이라는 변환 팩터를 재사용해서,
548*12 = 193 mod 491 = S
S = 193인 Superincreasing Key를 구합니다.
120+57+14+2 = 193
120, 57, 14, 2를 고른 경우 1로 선택한다고 하면,
| 개인키 | 2 | 3 | 7 | 14 | 30 | 57 | 120 | 251 |
| 복호화 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
다시 원문이었던 10010110 이 공개키로부터 복원됐습니다!!
...
비대칭키 암호화 알고리즘에서 가장 중요한 점은, A가 공개키를 모든 사람에게 뿌리고,
누군가가 A키의 공개키로 암호화 한 메시지는 A의 개인키로만 열어볼 수 있다는 것입니다.
...
3. 대칭키와 비대칭키에 관한 오해
비대칭키는 대칭키에 비해 매우 합리적인 것 처럼 보입니다. 따라서 다음과 같은 오해를 할 수도 있습니다.
Q1) 비대칭키는 대칭키 암호보다 더 안전하다?
아닙니다. 두 방식 모두 안전성은 이것을 깨기 위한 계산의 양에 달려있습니다.
Q2) 비대칭키는 대칭키 암호를 쓸모 없는 것으로 만들었다?
아닙니다. 비대칭키는 대칭키보다 연산의 양이 훨씬 많습니다. 이는 비대칭키 연산의 최대 약점입니다.
Q3) 비대칭키의 공개키 분배는 쉬운 일이다?
아닙니다. 비대칭키 암호의 생성 절차 자체가 대칭키 암호보다 간단하거나 효율적이지 않습니다. 따라서 공개키의 분배를 위해선 공개키 구조가 필요합니다.
...
설명이 길어졌습니다.
그럼 본격적인!! SSL암호화 방식은 다음 포스팅에서 써보겠습니다.
'내가 배운 것들' 카테고리의 다른 글
| [정보보호] AES알고리즘 중, MIX Column 계산하는 법 (6) | 2021.10.03 |
|---|---|
| [JAVA&OOP] 1~2강. 자바의 쓰임새와 객체에 대해서 (0) | 2021.03.03 |
0. 잡설
이번에 배포를 위한 서버를 제작하던 중, 보안에 대한 이슈가 많았습니다.
기존 개인 프로젝트를 하면서 신경쓰지 않았던 부분이라 좋은 경험을 하게 되었습니다.
HTTPS, 즉 SSL보안을 적용시켜야 한다고 생각했고, 이에 관해 동작 원리를 알고 싶어 정리합니다.
'정보보호'과목에서 배웠던 이론을 기초로 나름 제 언어로 정리해보겠습니다.
1. SSL(HTTPS)보안이 필요한 이유
2학년 시절, 간단한 웹소켓 채팅 웹을 만들어 Wire shark로 패킷을 검사해보는 프로젝트가 있었습니다.
SSL보안을 적용하지 않고 HTTP로 프로젝트를 진행했었습니다.
HTTPS로는 패킷 검사하는 것이 힘드니까요.
HTTP로 접속했을 때 패킷을 중간에 누군가가 까본다면 어떻게 보일까요?

이렇게 왼쪽 msg처럼, "안녕하세요"라는 패킷이 그대로 복원이 됨을 알 수 있습니다.
패킷에 비밀번호가 그대로 전달되거나, token이라도 전달된다면 중간자가 사용자 행세를 할 수도 있겠습니다(이를 Packet sniffing 공격이라고 합니다).
따라서 우리는 클라이언트와 서버가 비밀통로로 연결되는 SSL보안 연결이 필요합니다.
2. 대칭키와 비대칭키
SSL연결은 기본적으로 비대칭키로 암호화를 진행하지만, 우선 연결이 되면 대칭키로 빠르게 내용을 주고 받으므로 두개의 개념을 모두 알고 있어야 합니다.
대칭키
어떤 문장을 암호화 하는 사람과 해독하는 사람(복호화)하는 사람이 모두 같은 키를 사용하는 방식입니다.
예를 들어, 시저 암호화가 있습니다. 알파벳이 있다면, 3글자씩 밀려 써서 암호화를 하는 방식입니다.
표로 살펴보겠습니다.
| 원문 | A | B | C | D | E | ... | X | Y | Z |
| 암호화시 | D | E | F | G | H | ... | A | B | C |
만약 시저 암호화를 한 메시지가 다음과 같았다고 합시다.
L FDPH L VDZ L FRQTXHUNG
암호화는 각 알파벳을 3칸 밀어서 쓴다는 것을 아는 해독자는 이를 다음과 같이 복호화 할 수 있습니다.
I CAME I SAW CONQUERED
대칭키 암호화의 원리는 이렇습니다. 암호화하는 방식과 복호화 하는 방식(키)이 동일한 것입니다.
물론, 현대에는 비트를 알고리즘에 의해 옮기는 방법으로 더 복잡합니다. 하지만 이 역시도 알고리즘이 공개되어있기 때문에 brute force공격을 하면 언젠가는 뚫리게 되어 있습니다.
현대 암호를 풀려면 얼마나 시간이 걸릴까요?
현대적인 대칭키 암호화 방식인 DES를 3중으로 쌓으면 2^112의 brute force공격이 필요합니다.
이는 이정도의 크기를 가집니다.

아주아주 좋은 컴퓨터가 저 만큼만 brute force공격을 한다면 대칭키는 뚫리게 되는 것이죠!
은행 보안 카드가 몇 초에 한번씩 업데이트되는 이유가 여기에 있습니다. 아주아주 좋은 컴퓨터가 브루트포스로 공격을 진행해도, 결과가 나오기 전에 키를 바꾸어 버리는 것이지요!
. . .
이 방식은 정해진 몇개의 암/복호화 알고리즘을 수학적으로 따르면 되므로, 속도가 빠릅니다.
하지만, 암호를 전달하는 과정에서 키가 탈취되는 문제가 있습니다. 암호 키를 전달하는 과정 자체에서 암호키가 가로채질 수 있다는 것입니다.
장점: 암/복호화가 빠르다
단점: 키 전달 과정에서 탈취될 수 있다.
비대칭키
공개키 알고리즘이라고도 합니다. 공개키 알고리즘이 더욱 와닿으니 앞으로 공개키라고 설명하겠습니다.
어떤 메시지를 암호화해야한다고 합시다. 비대칭키 알고리즘에서는 개인키/공개키로 암호화됩니다.
어떤 메시지가 Alice에 의해 암호화된다고 할 때, 메시지는 Alice의 공개키로 암호화되고, 복호화 시에는 Alice의 개인키로만 복호화될 수 있습니다.
누구나 Alice의 공개키를 가질 수 있어 Bob도, 스폰지밥도, 징징이도 암호화를 할 수 있지만 메시지의 복호화는 Alice만이 가지고 있는 개인키로만 가능합니다. Alice만 읽을 수 있게 되는 것이죠!
공개키는 단방향 함수로 암호화됩니다. 단방향 함수라 함은, 한 방향으로 계산은 쉬우나 반대 방향으로의 계산은 어려운 함수를 의미합니다.
예를 들어, 3*17 = 51이라는 것은 아주 쉬우나, 51 = 3*17이라는 사실은 알아내기 매우 어렵습니다.
N=pq라는 계산은 용이하지만 N이 주어졌을 때 P와 Q를 알아내는 것은 쉽지 않은 것이 단반향 함수입니다.
비대칭키에 대한 가장 유명한 방식은 RSA방식입니다. 바로 RSA방식에 대해 공부하면 머리가 아플 수 있으므로, 이해하기 쉬운 냅색 문제로 비대칭키 암호화를 하는 경우를 보겠습니다.
냅색 문제와 비대칭키 알고리즘
냅색 문제란?
가중치 집합 {62, 93, 26, 52, 166, 48, 91, 141}이 주어졌다고 합시다.
가중치 집합의 원소를 합쳐서 302이 되는 subset을 찾아봅시다.
일반적으로 냅색 문제는 NP-complete입니다. 어떤 문제가 NP-complete라는 말은, 그 문제를 시간만 많이 주면 풀어낼 순 있지만 문제의 답을 찾는 알고리즘은 밝혀지지 않았다는 뜻입니다. 더 쉽게 말하면 인간은 풀 수 있지만 컴퓨터로는 못푸는 문제라고 생각할 수 있습니다.
위의 문제의 답은 62+26+166+48 = 302 입니다.
냅색 문제를 쉽게 풀어내는 방법은 superincreasing knapsack문제로 바꾸어 푸는 것입니다. 이는 "새로운 가중치는 모든 이전 가중치의 합 보다 크다"라는 의미입니다.
예를 들어 가중치 집합이 {2, 3, 7, 14, 30, 57, 120, 251}인 경우
이 방법으로 합이 186인 subset을 찾는 문제의 답은 2+7+57+120 = 186입니다.
이제 본격적으로 냅색 알고리즘을 활용하여 암호화를 해보겠습니다.
공개키는 가중치 집합이고,
개인키는 공개키를 Superincreasing knapsack문제로 풀어낸 집합과 conversion factor입니다.
예를 들어, 본인이 Superincreasing kanpsack문제의 해 집합을 가지고 있다고 해봅시다.
superincreasing Key = {2, 3, 7, 14, 30, 57, 120, 251}
또한 m=41, n=491, 1/m % n = 41^-1 mod 491 = 12이라는 변환 팩터를 가지고 있습니다.
이 키와 변환 팩터를 가지고 다음과 같이 공개키를 제작할 수 있습니다.
2 X 41 mod 491 = 82
3 X 41 mod 491 = 123
7 X 41 mod 491 = 287
14 X 41 mod 491 = 83
...
120 X 41 mod 491 = 10
251 X 41 mod 491 = 471
그러면 공개키는 다음과 같습니다.
공개키: {82, 123, 287, 83, 248, 373, 10, 471}
그럼 이를 어떻게 써먹을 수 있을까요??
예를 들어 10010110을 암호화 한다고 합시다.
| 공개키 | 82 | 123 | 287 | 83 | 248 | 373 | 10 | 471 |
| 평문 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
암호화 결과는 82 + 83 + 373 + 10 = 548입니다.
그럼 548로 암호화된 키를 복호화 하려면 다음과 같이 하면 됩니다.
개인키 = {2, 3, 7, 14, 30, 57, 120, 251}
또한 m=41, n=491, 1/m % n = 41^-1 mod 491 = 12이라는 변환 팩터를 재사용해서,
548*12 = 193 mod 491 = S
S = 193인 Superincreasing Key를 구합니다.
120+57+14+2 = 193
120, 57, 14, 2를 고른 경우 1로 선택한다고 하면,
| 개인키 | 2 | 3 | 7 | 14 | 30 | 57 | 120 | 251 |
| 복호화 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
다시 원문이었던 10010110 이 공개키로부터 복원됐습니다!!
...
비대칭키 암호화 알고리즘에서 가장 중요한 점은, A가 공개키를 모든 사람에게 뿌리고,
누군가가 A키의 공개키로 암호화 한 메시지는 A의 개인키로만 열어볼 수 있다는 것입니다.
...
3. 대칭키와 비대칭키에 관한 오해
비대칭키는 대칭키에 비해 매우 합리적인 것 처럼 보입니다. 따라서 다음과 같은 오해를 할 수도 있습니다.
Q1) 비대칭키는 대칭키 암호보다 더 안전하다?
아닙니다. 두 방식 모두 안전성은 이것을 깨기 위한 계산의 양에 달려있습니다.
Q2) 비대칭키는 대칭키 암호를 쓸모 없는 것으로 만들었다?
아닙니다. 비대칭키는 대칭키보다 연산의 양이 훨씬 많습니다. 이는 비대칭키 연산의 최대 약점입니다.
Q3) 비대칭키의 공개키 분배는 쉬운 일이다?
아닙니다. 비대칭키 암호의 생성 절차 자체가 대칭키 암호보다 간단하거나 효율적이지 않습니다. 따라서 공개키의 분배를 위해선 공개키 구조가 필요합니다.
...
설명이 길어졌습니다.
그럼 본격적인!! SSL암호화 방식은 다음 포스팅에서 써보겠습니다.
'내가 배운 것들' 카테고리의 다른 글
| [정보보호] AES알고리즘 중, MIX Column 계산하는 법 (6) | 2021.10.03 |
|---|---|
| [JAVA&OOP] 1~2강. 자바의 쓰임새와 객체에 대해서 (0) | 2021.03.03 |