지극히 주관적인 [모두의 딥러닝 시즌 2] 강좌 리뷰입니다.
개인적으로 몰랐던 부분, 알게된 부분을 중점으로 작성하였습니다.
1. 파이토치 인덱싱

넘파이의 인덱싱 과정과 같습니다. 가장 기본적인 연산입니다.

다음과 같은 벡터를 생성해봅시다. a = [0, 1, 2, 3, 4, 5]입니다.
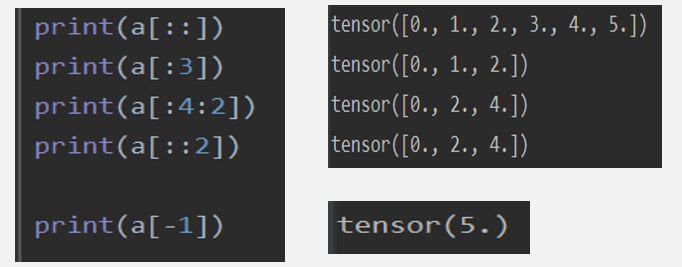
각 연산 결과는 바로 옆에 위치한 사진과 같습니다.
- a[::] 인덱싱 : 시작이 없으므로 0번째부터, 끝이 없으므로 맨 뒤까지, 점프가 없으므로 기본값인 1이 설정되어
[0, 1, 2, 3, 4, 5]가 출력되었습니다. - a[:3] 인덱싱 : 시작이 없으므로 0번째부터, 3번 인덱스까지 1씩 점프하였으므로, [0, 1, 2]가 출력되었습니다.
- a[:4:2] 인덱싱 : 시작이 없으므로 0번째부터, 4번째 인덱스까지 2씩 점프하였으므로 [0, 2, 4]가 출력되었습니다.
- a[::2] 인덱싱 : 시작이 없으므로 0번째부터, 끝이 없으므로 맨 뒤까지, 점프가 2이므로 [0, 2, 4]가 출력되었습니다.
- a[-1] 인덱싱 : 음수 인덱싱을 주변 맨 뒤부터 반환됩니다. 맨뒤가 -1부터 시작합니다.
2. 파이토치 Dimension
파이토치가 지원하는 각 연산에서 Dimension 연산도 많이 수행합니다.
차원이 없는 것을 스칼라, 1차원을 지닌 것을 벡터, 2차원을 지닌 것을 행렬, 3차원을 지닌 것을 텐서라고 합니다.
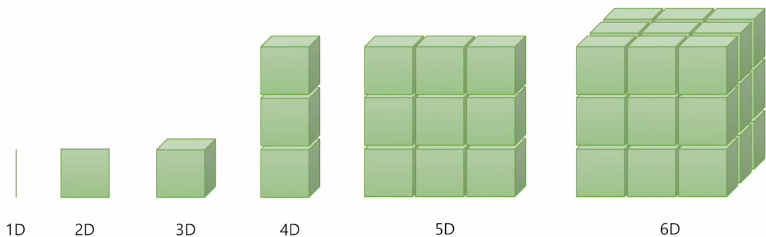
연산에서 Dim=n(주로 n은 0~3의 범위)을 파라미터로 주는 경우가 꽤 있습니다.
개인적으로, 차원은 1차원부터 시작인데 왜 Dim=0을 주는 경우가 있을까? 라는 의문이 있습니다. 저와 비슷한 의문을 가지셨던 분들이 있다면, 다음 정의와 사진을 보시면 이해가 쉬우실 것 같습니다.
Dim 연산은, Shape를 출력했을 때 해당 텐서의 인덱스와 같습니다.
흠.. 더 헷갈리는 것 같습니다. 예시를 보면서 제가 내린 정의를 다시 보면 이해가 될 것입니다.
다음과 같은 행렬을 선언해 보겠습니다.

shape를 출력해보면, [3, 5]를 출력합니다.
print(b.sum(dim=0))
print(b.sum(dim=1))
print(b.sum(dim=-1))위 연산을 수행하면, 다음과 같은 결과가 출력됩니다.

- b.sum(dim=0)연산의 수행 결과: b.shape의 결과인 [3, 5] 중 0번째 인덱스인 3, 즉 col축을 기준으로 한 연산을 수행했음을 볼 수 있습니다.
- b.sum(dim=1)연산의 수행 결과: b.shape의 결과인 [3, 5] 증 1번째 인덱스인 5, 즉 row축을 기준으로 한 연산을 수행했음을 볼 수 있습니다.
- b.sum(dim=-1)연산의 수행 결과: 음수 인덱싱은 맨 뒤가 -1부터 시작하는 인덱싱 방식입니다. b.sum(dim=-1)의 결과와 동일합니다.
3. Linear Regression
이제부터 본격적인 입문 시작입니다. 가장 간단한 형태의 학습 방식에 대해 알아보겠습니다.
다음과 같은 공부 시간과 성적 사이의 관계가 있다고 가정합시다. 공부를 얼마나 하면 몇점 정도의 성적을 받게될지가 궁금합니다.
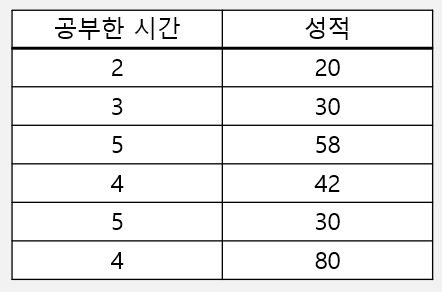
확실히 공부를 많이 하면 성적을 잘 받는 것 같습니다. 대충 공부 한 시간의 10배정도의 성적을 받는 것 같은데, 적게 공부하고도 성적을 잘 받는 사람이 있고, 많이 공부했는데도 성적을 못받은 사람도 있어 둘 사이의 관계식을 정확하게 규명하기가 어렵습니다.
그래서 둘 사이의 관계를 규명하기 위해 다음과 같은 식을 세워봅니다.

공부한 시간을 X로 생각하고, W와 B는 미지수로 설정합니다. W와 B를 브루트 포스를 이용해 찾다보면 언젠가는 답을 찾을 수 있을 것 같습니다. 모두를 만족시키진 못해도, 대충 분포에 맞는 그래프를 찾을 수 있겠습니다.
그런데, 지금 내가 세운 가설이 [대충 분포에 맞는 그래프]인지 어떻게 알 수 있다는 것 일까요? 다음과 같은 식으로 가설이 낸 오류를 구할 수 있습니다.

가설과 결과의 차이를 제곱하여 음수가 나올 가능성을 제합니다. 이후 평균을 구하면, 내가 이번 경우에 얼마나 예측을 잘했는지 알 수 있습니다.
파이토치 코드로 쓰면 다음과 같습니다.
Cost = torch.mean((hypothesis-y)**2)mean 함수는 평균을 구하는데 사용하는 함수입니다.
다시 예시로 돌아가서, 공부한 시간에 대한 점수를 구하는 코드를 보겠습니다.
import numpy as np
import torch
from torch import optim
x_train = torch.FloatTensor([[2], [3], [5], [4], [5], [4]])
y_train = torch.FloatTensor([[20], [30], [58], [42], [30], [80]])
W = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
optimizer = optim.SGD([W, b], lr=0.015)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
hypothesis = x_train * W + b
cost = torch.mean((hypothesis - y_train) ** 2)
if epoch % 100 == 0:
print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(
epoch, nb_epochs, W.item(), b.item(), cost.item()
))
optimizer.zero_grad()
cost.backward()
optimizer.step()
x_train: 데이터
y_train: 결과
W, b: 미지수. requires_grad=True를 주어 이 변수가 Gradient Descent의 결과에 따라 변화함을 나타냅니다.
Optimizer: SGD방식에 따라 W와 b를 최적화합니다. SGD에 대해선 다음 장에 알아봅니다.
epoch: 학습 데이터 전체를 한번 학습하면 1 epoch가 지났다고 할 수 있습니다.
※SGD란? 확률적 경사 하강법으로, 데이터 Set에서 무작위로 선택한 하나의 예에 의존하여 각 단계의 예측 경사를 계산하는 방식. 전체를 학습하는 방식보단 확실히 빠르지만, 랜덤으로 예시를 학습하므로 매우 예외적인 예를 선택할 수도 있음.
[항상 붙어다니는 3인방]
optimizer.zero_grad()
cost.backward()
optimizer.step()위 코드에서 볼 수 있는 이 3인방은 강의에서 '항상 붙어다니는 3인방'이라고 불렸습니다.
각각의 역할은 다음과 같습니다.
- optimizer.zero_grad(): 파이토치는 각각의 계산 후 optimizer를 초기화 하지 않습니다. 이 코드를 통해 각 학습마다 초기화해줍니다.
- cost.backward(): cost함수를 계산하여 Gradient를 계산합니다.
- optimzer.step(): W와 B를 업데이트합니다.
'머신러닝' 카테고리의 다른 글
| [Pytorch] Siamese network를 이용하여 나의 외모를 점검해보자_2탄 (1) | 2021.02.27 |
|---|---|
| [Pytorch] Siamese network를 이용하여 나의 외모를 점검해보자_1탄 (1) | 2021.02.17 |
| [Pytorch] 데이터를 뻥튀기하자! Data Augmentation (8) | 2021.02.13 |
지극히 주관적인 [모두의 딥러닝 시즌 2] 강좌 리뷰입니다.
개인적으로 몰랐던 부분, 알게된 부분을 중점으로 작성하였습니다.
1. 파이토치 인덱싱

넘파이의 인덱싱 과정과 같습니다. 가장 기본적인 연산입니다.

다음과 같은 벡터를 생성해봅시다. a = [0, 1, 2, 3, 4, 5]입니다.

각 연산 결과는 바로 옆에 위치한 사진과 같습니다.
- a[::] 인덱싱 : 시작이 없으므로 0번째부터, 끝이 없으므로 맨 뒤까지, 점프가 없으므로 기본값인 1이 설정되어
[0, 1, 2, 3, 4, 5]가 출력되었습니다. - a[:3] 인덱싱 : 시작이 없으므로 0번째부터, 3번 인덱스까지 1씩 점프하였으므로, [0, 1, 2]가 출력되었습니다.
- a[:4:2] 인덱싱 : 시작이 없으므로 0번째부터, 4번째 인덱스까지 2씩 점프하였으므로 [0, 2, 4]가 출력되었습니다.
- a[::2] 인덱싱 : 시작이 없으므로 0번째부터, 끝이 없으므로 맨 뒤까지, 점프가 2이므로 [0, 2, 4]가 출력되었습니다.
- a[-1] 인덱싱 : 음수 인덱싱을 주변 맨 뒤부터 반환됩니다. 맨뒤가 -1부터 시작합니다.
2. 파이토치 Dimension
파이토치가 지원하는 각 연산에서 Dimension 연산도 많이 수행합니다.
차원이 없는 것을 스칼라, 1차원을 지닌 것을 벡터, 2차원을 지닌 것을 행렬, 3차원을 지닌 것을 텐서라고 합니다.

연산에서 Dim=n(주로 n은 0~3의 범위)을 파라미터로 주는 경우가 꽤 있습니다.
개인적으로, 차원은 1차원부터 시작인데 왜 Dim=0을 주는 경우가 있을까? 라는 의문이 있습니다. 저와 비슷한 의문을 가지셨던 분들이 있다면, 다음 정의와 사진을 보시면 이해가 쉬우실 것 같습니다.
Dim 연산은, Shape를 출력했을 때 해당 텐서의 인덱스와 같습니다.
흠.. 더 헷갈리는 것 같습니다. 예시를 보면서 제가 내린 정의를 다시 보면 이해가 될 것입니다.
다음과 같은 행렬을 선언해 보겠습니다.

shape를 출력해보면, [3, 5]를 출력합니다.
print(b.sum(dim=0))
print(b.sum(dim=1))
print(b.sum(dim=-1))위 연산을 수행하면, 다음과 같은 결과가 출력됩니다.

- b.sum(dim=0)연산의 수행 결과: b.shape의 결과인 [3, 5] 중 0번째 인덱스인 3, 즉 col축을 기준으로 한 연산을 수행했음을 볼 수 있습니다.
- b.sum(dim=1)연산의 수행 결과: b.shape의 결과인 [3, 5] 증 1번째 인덱스인 5, 즉 row축을 기준으로 한 연산을 수행했음을 볼 수 있습니다.
- b.sum(dim=-1)연산의 수행 결과: 음수 인덱싱은 맨 뒤가 -1부터 시작하는 인덱싱 방식입니다. b.sum(dim=-1)의 결과와 동일합니다.
3. Linear Regression
이제부터 본격적인 입문 시작입니다. 가장 간단한 형태의 학습 방식에 대해 알아보겠습니다.
다음과 같은 공부 시간과 성적 사이의 관계가 있다고 가정합시다. 공부를 얼마나 하면 몇점 정도의 성적을 받게될지가 궁금합니다.

확실히 공부를 많이 하면 성적을 잘 받는 것 같습니다. 대충 공부 한 시간의 10배정도의 성적을 받는 것 같은데, 적게 공부하고도 성적을 잘 받는 사람이 있고, 많이 공부했는데도 성적을 못받은 사람도 있어 둘 사이의 관계식을 정확하게 규명하기가 어렵습니다.
그래서 둘 사이의 관계를 규명하기 위해 다음과 같은 식을 세워봅니다.

공부한 시간을 X로 생각하고, W와 B는 미지수로 설정합니다. W와 B를 브루트 포스를 이용해 찾다보면 언젠가는 답을 찾을 수 있을 것 같습니다. 모두를 만족시키진 못해도, 대충 분포에 맞는 그래프를 찾을 수 있겠습니다.
그런데, 지금 내가 세운 가설이 [대충 분포에 맞는 그래프]인지 어떻게 알 수 있다는 것 일까요? 다음과 같은 식으로 가설이 낸 오류를 구할 수 있습니다.

가설과 결과의 차이를 제곱하여 음수가 나올 가능성을 제합니다. 이후 평균을 구하면, 내가 이번 경우에 얼마나 예측을 잘했는지 알 수 있습니다.
파이토치 코드로 쓰면 다음과 같습니다.
Cost = torch.mean((hypothesis-y)**2)mean 함수는 평균을 구하는데 사용하는 함수입니다.
다시 예시로 돌아가서, 공부한 시간에 대한 점수를 구하는 코드를 보겠습니다.
import numpy as np
import torch
from torch import optim
x_train = torch.FloatTensor([[2], [3], [5], [4], [5], [4]])
y_train = torch.FloatTensor([[20], [30], [58], [42], [30], [80]])
W = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
optimizer = optim.SGD([W, b], lr=0.015)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
hypothesis = x_train * W + b
cost = torch.mean((hypothesis - y_train) ** 2)
if epoch % 100 == 0:
print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(
epoch, nb_epochs, W.item(), b.item(), cost.item()
))
optimizer.zero_grad()
cost.backward()
optimizer.step()
x_train: 데이터
y_train: 결과
W, b: 미지수. requires_grad=True를 주어 이 변수가 Gradient Descent의 결과에 따라 변화함을 나타냅니다.
Optimizer: SGD방식에 따라 W와 b를 최적화합니다. SGD에 대해선 다음 장에 알아봅니다.
epoch: 학습 데이터 전체를 한번 학습하면 1 epoch가 지났다고 할 수 있습니다.
※SGD란? 확률적 경사 하강법으로, 데이터 Set에서 무작위로 선택한 하나의 예에 의존하여 각 단계의 예측 경사를 계산하는 방식. 전체를 학습하는 방식보단 확실히 빠르지만, 랜덤으로 예시를 학습하므로 매우 예외적인 예를 선택할 수도 있음.
[항상 붙어다니는 3인방]
optimizer.zero_grad()
cost.backward()
optimizer.step()위 코드에서 볼 수 있는 이 3인방은 강의에서 '항상 붙어다니는 3인방'이라고 불렸습니다.
각각의 역할은 다음과 같습니다.
- optimizer.zero_grad(): 파이토치는 각각의 계산 후 optimizer를 초기화 하지 않습니다. 이 코드를 통해 각 학습마다 초기화해줍니다.
- cost.backward(): cost함수를 계산하여 Gradient를 계산합니다.
- optimzer.step(): W와 B를 업데이트합니다.
'머신러닝' 카테고리의 다른 글
| [Pytorch] Siamese network를 이용하여 나의 외모를 점검해보자_2탄 (1) | 2021.02.27 |
|---|---|
| [Pytorch] Siamese network를 이용하여 나의 외모를 점검해보자_1탄 (1) | 2021.02.17 |
| [Pytorch] 데이터를 뻥튀기하자! Data Augmentation (8) | 2021.02.13 |